Summer@ICERM 2020: Efficient Eigensolvers And Their Applications

Yuqing Liu University of Michigan Ann Arbor

Kelly Rivera St. Thomas University

Jordan Fox Western Carolina University

Welcome to our webpage for Efficient Eigensolvers!

This summer, we are working on solving eigenvectors and eigenvalues for a given matrix. Based on the non-existance of the closed formula for the root of an arbitrary polynomial with degree 5 or more, we conclude there is no eigensolver that could solve the eigenvalues for an arbitrary matrix in finite steps even given the perfect accuracy.

Numerically, eigensolvers must be iterative.

In this project, we implemented variant eigensolvers, built up web crawlers with directed graph generator, constructed performance comparison code frame.

For numerical experiments results, we collected page rank scores for subpages under several domains: https://icerm.brown.edu, https://en.wikipedia.com/wiki/, https://cnn.com/, etc. You can find the adjacency matrices and page rank results here.

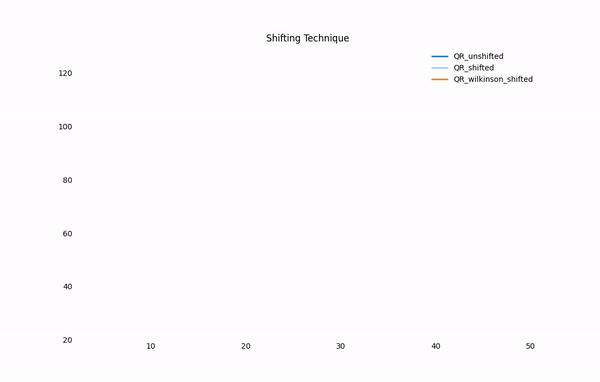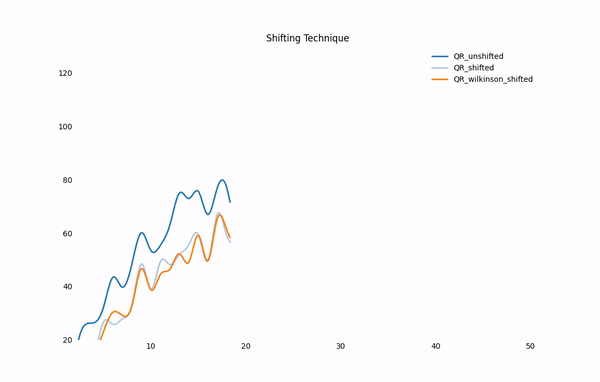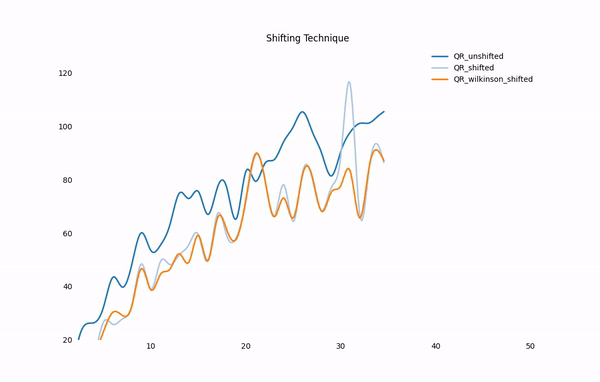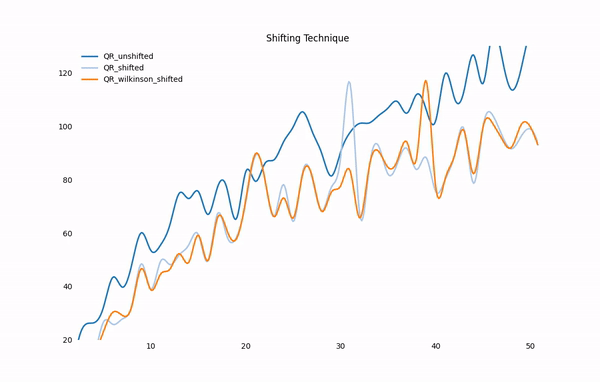
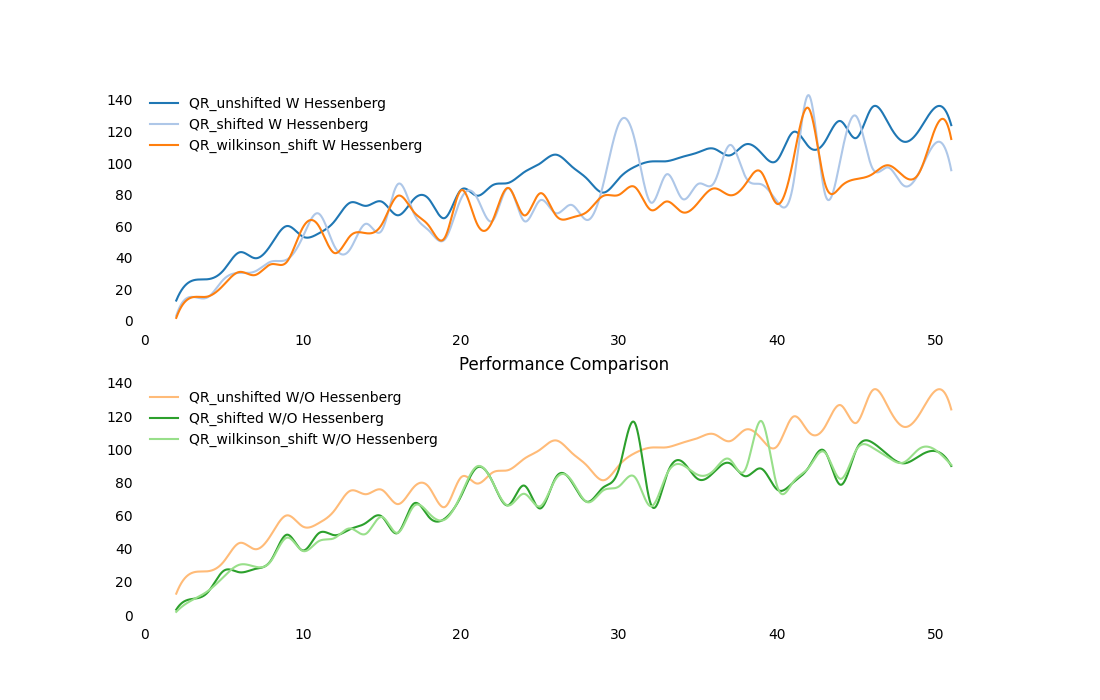
To see how preprocessing a matrix like applying reduction could save the run time, we measured convergence rates for different eigensolvers with and without Hessenberg Reduction.

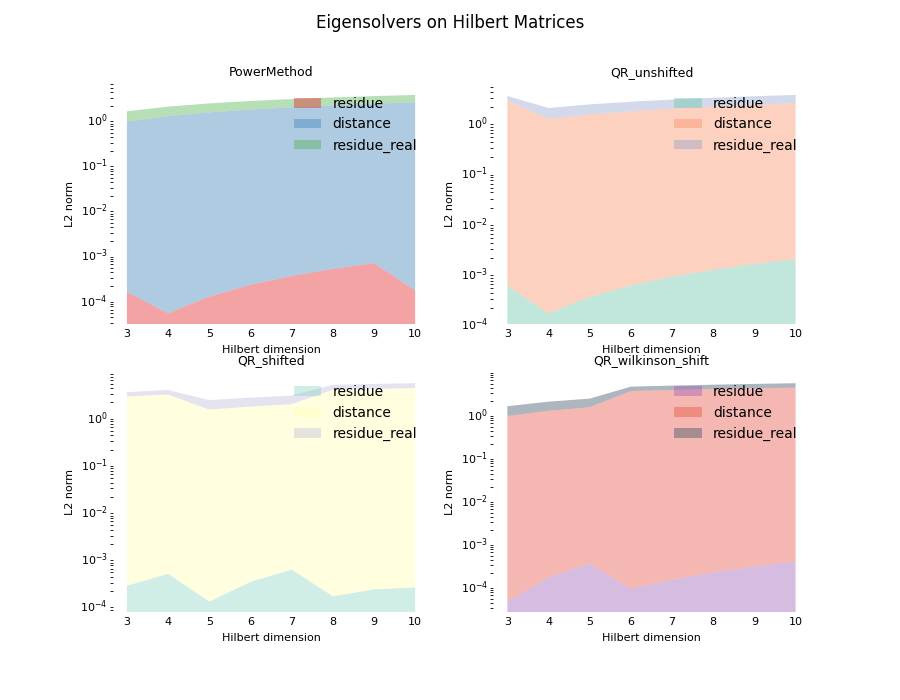
Hilbert matrix, a nightmare for generations of scientists working on improving the time complexity of the eigensolver, is revisited by our code. We visualized how bad our eigensolvers are when facing this accuracy dilemma caused by Hilbert matrix.

Eigensolvers

We implemented two major kinds of eigensolvers:

• based on converged sequences.
  • Power Iteration
  • Inverse Iteration without/with Shift
• based on Eigenvalue-revealing factorizations. For example, Schur diagonalization.
  • QR Algorithm

We also introduced other variants involving different techniques, e.g. Rayleigh Quotient Iteration.

Webcrawler

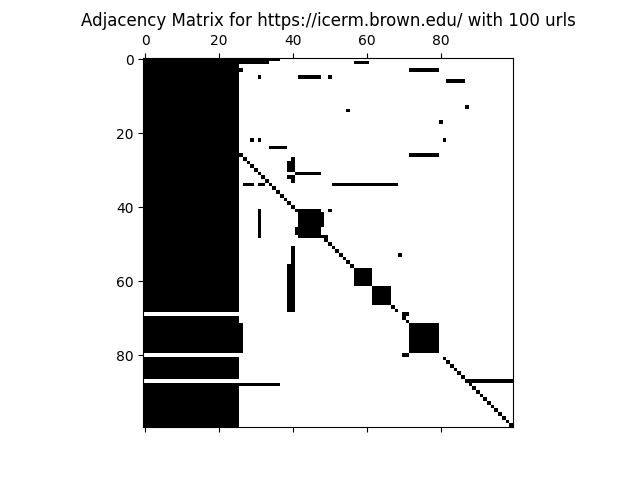
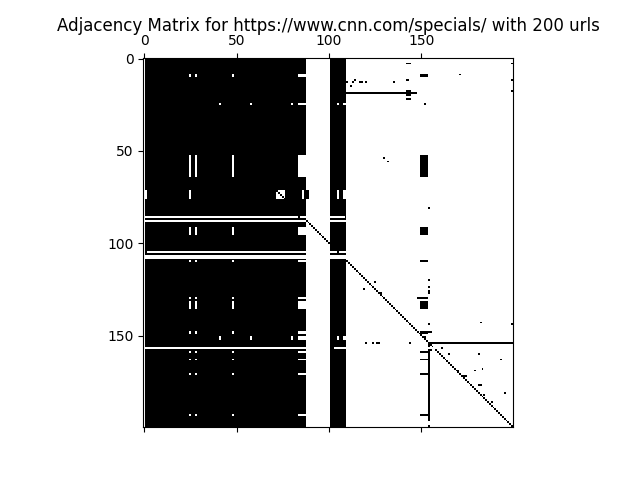
A common application for eigensolvers, more specifically, Power Iteration Method, is PageRank. By crawling all the subpages under a given domain, we generated a directed graph with vertices representing subpages and directed edges representing linkages by webcrawler. By manipulating this directed graph’s adjacency matrix and feeding it into the eigensolver, we could converge to the dominant eigenvalue’s eigenvectors, where each value could be regarded as an importance score.

Let’s rank!

• https://icerm.brown.edu/ : Page Rank Scores
• https://cnn.com/specials/ : Page Rank Scores

Performance Experiments

Hessenberg Reduction with Shift

The time complexity for each plain eigensolver is O(n^3), which is problematic for actual applications – when we are crawling 10 million pages and processing a 10 million dimensional matrix – the time consumed is not fun. Hessenberg Reduction comes to help.

Hilbert Matrix

Let’s face the tricky Hilbert matrix.

Side notes:

if you also want to know how to …

• generate a random matrix
• implement adaptive page rank algorithm
• manipulate the adjacency matrix in Page Rank algorithms
• test the correctness for different algorithms